Introduction:
Cross-validation is a crucial aspect of the data science workflow, playing a pivotal role in model evaluation, validation techniques, hyperparameter tuning, and managing the bias-variance tradeoff. In this comprehensive guide, we will delve into the intricacies of cross-validation, exploring its importance and various techniques.
What is Cross-Validation?
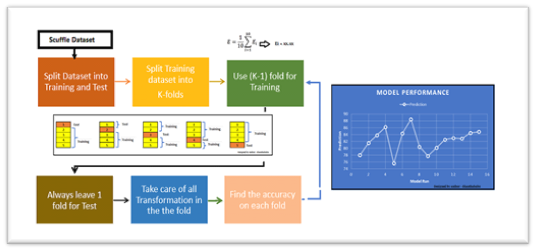
Cross-validation is a statistical technique used to assess how well a machine learning model will generalize to an independent dataset. It involves partitioning the dataset into subsets, training the model on some of these subsets, and evaluating its performance on the remaining data. The process helps in understanding how well the model will perform on unseen data, providing insights into potential issues like overfitting or underfitting.
Model Evaluation:
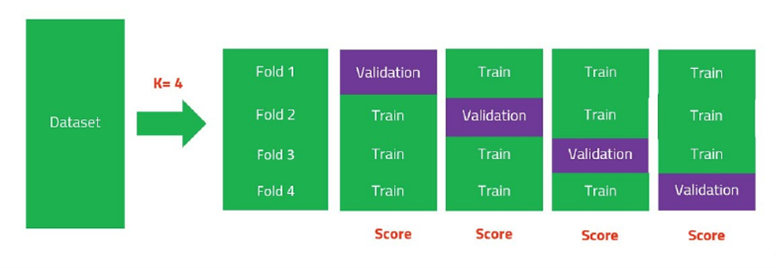
- K-Fold Cross-Validation:
One of the most common cross-validation techniques is K-Fold Cross-Validation. In this method, the dataset is divided into ‘K’ subsets (or folds), and the model is trained ‘K’ times, each time using a different fold for evaluation and the remaining folds for training. The results are averaged to obtain a more robust performance estimate.
- Stratified K-Fold Cross-Validation:
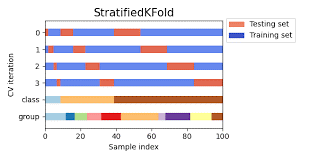
Stratified K-Fold Cross-Validation is especially useful when dealing with imbalanced datasets. It ensures that each fold maintains the same distribution of target classes as the original dataset, providing a more representative evaluation.
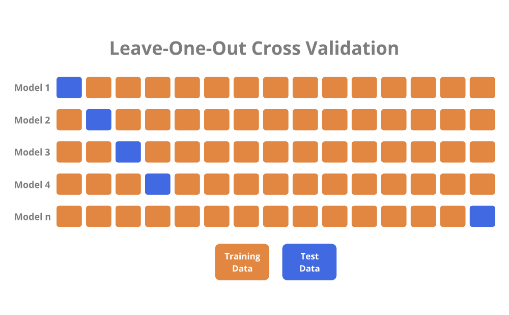
- Leave-One-Out Cross-Validation (LOOCV):
In LOOCV, only one data point is used as the test set while the rest of the data is used for training. This process is repeated for each data point. While LOOCV provides a comprehensive evaluation, it can be computationally expensive for large datasets.
Validation Techniques:
- Holdout Validation:
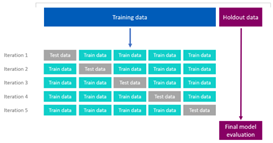
Holdout validation involves splitting the dataset into two parts: a training set and a validation set. The model is trained on the training set, and its performance is assessed on the validation set. This approach is simple but may lead to variability in the evaluation depending on the random split.
- Time Series Cross-Validation:
For time-dependent data, such as stock prices or weather patterns, Time Series Cross-Validation is crucial. It ensures that training and validation sets maintain the temporal order, reflecting the real-world scenario where predictions are made on future data based on past observations.
Hyperparameter Tuning
Cross-validation is integral to hyperparameter tuning, allowing data scientists to find the optimal configuration for a model. By systematically adjusting hyperparameters and assessing performance across multiple folds, one can identify the combination that results in the best generalization.
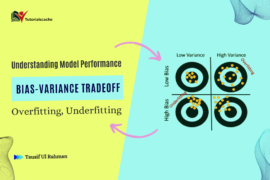
Bias-Variance Tradeoff:
Cross-validation aids in managing the bias-variance tradeoff by providing a quantitative measure of a model’s ability to generalize. If a model performs well on the training data but poorly on the validation data, it might be overfitting (high variance). On the other hand, consistently poor performance on both sets might indicate underfitting (high bias).
Conclusion:
Cross-validation is an indispensable tool in a data scientist’s arsenal, offering insights into a model’s generalization capabilities, aiding in hyperparameter tuning, and helping strike the right balance between bias and variance. By understanding the various cross-validation techniques and their applications, data scientists can enhance the reliability and robustness of their machine learning models.